前言

龙强-最优化理论与算法课程。21年免费课程上有许多的笔误口误，但瑕不掩瑜——这些错误，都比较容易看出来。25年付费课程，我没看过。

最优化基础

Taylor 展开式

梯度（一阶偏导数向量）：

$$\bigtriangledown f(x) = (\frac {\partial f}{\partial x_1}, \frac {\partial f}{\partial x_2}, \cdots, \frac {\partial f}{\partial x_n})$$

Hesse 矩阵（二阶偏导数矩阵）：

$$H(x) = \bigtriangledown^2 f(x) = \begin{pmatrix} \frac {\partial^2 f}{\partial x_1^2} & \frac {\partial^2 f}{\partial x_2x_1} & \cdots & \frac {\partial^2 f}{\partial x_nx_1} \\ \frac {\partial^2 f}{\partial x_1x_2} & \frac {\partial^2 f}{\partial x_2^2} & \cdots & \frac {\partial^2 f}{\partial x_nx_2} \\ \vdots & \vdots & \ddots & \vdots \\ \frac {\partial^2 f}{\partial x_1x_n} & \frac {\partial^2 f}{\partial x_2x_n} & \cdots & \frac {\partial^2 f}{\partial x_n^2} \\ \end{pmatrix}$$

• 线性函数：$f(x) = c^T x + b,\quad\bigtriangledown f(x) = c,\quad\bigtriangledown^2 f(x) = 0$
• 二次函数：$f(x) = \frac{1}{2} x^TQx + c^T x + b,\quad\bigtriangledown f(x) = Qx + c,\quad\bigtriangledown^2 f(x) = Q$（对称）

Jacobi 矩阵（对向量值函数求梯度）：

考虑向量值函数 $h(x) = (\ h_1(x),\ h_2(x),\ \cdots,\ h_m(x)\ )^T$ ，其中每个分量 $h_i(x)$ 都是 n 元实值函数，假设对所有的 $i，j$ 偏导数 $\frac{\partial h_i(x)}{\partial x_j}$ 存在。$h$ 在点 $x$ 的 Jacobi 矩阵为

$$J(h) = \begin{pmatrix} \frac {\partial h_1(x)}{\partial x_1} & \frac {\partial h_1(x)}{\partial x_2} & \cdots & \frac {\partial h_1(x)}{\partial x_n} \\ \frac {\partial h_2(x)}{\partial x_1} & \frac {\partial h_2(x)}{\partial x_2} & \cdots & \frac {\partial h_2(x)}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac {\partial h_m(x)}{\partial x_1} & \frac {\partial h_m(x)}{\partial x_2} & \cdots & \frac {\partial h_m(x)}{\partial x_n} \\ \end{pmatrix} = \begin{pmatrix} \bigtriangledown h_1(x) \\ \bigtriangledown h_2(x) \\ \vdots \\ \bigtriangledown h_m(x) \\ \end{pmatrix}$$

这个矩阵称为向量值函数 $h$ 在 $x$ 处的导数。

$J(\bigtriangledown f) = H(x)^T$

n 元函数的 Taylor 展开式。设 $f(x): R^n \to R$ ，二阶可导，在 $x^*$ 的邻域内：

• 一阶 Taylor 展开式：

$$f(x) = f(x^*) + \bigtriangledown f^T(x^*)(x-x^*) + o\left\| x-x^* \right\|$$

• 二阶 Taylor 展开式：

$$f(x) = f(x^*) + \bigtriangledown f^T(x^*)(x-x^*) + \frac{1}{2}(x-x^*)^T\bigtriangledown^2 f(x^*)(x-x^*) + o\left\| x-x^* \right\|^2$$

一阶中值公式：对 $x,\exists \lambda \in (0,1)$ ，使

$$f(x) = f(x^*) + \bigtriangledown f^T(x^*+\lambda(x-x^*))(x-x^*)$$

Lagrange 余项：对 $x,\exists \mu \in (0,1)$ ，记 $x_\mu = x^* + \mu(x-x^*)$ ，使

$$f(x) = f(x^*) + \bigtriangledown f^T(x^*)(x-x^*) + \frac{1}{2}(x-x^*)^T\bigtriangledown^2 f(x_\mu)(x-x^*)$$

范数

向量范数的定义。若实值函数 $\|\ .\ \|: R^n \rightarrow R$ 满足下列条件：

1. $\|x\| \ge 0,\ \forall x \in R^n;\ \|x\| = 0\ 当且仅当\ x=0$
2. $\|\alpha x\| = |\alpha|\ \|x\|,\ \forall \alpha \in R,\ x \in R^n$
3. $\|x+y\| \le \|x\|\ + \|y\|,\ \forall \ x,y \in R^n$

则称 $\|\ .\ \|$ 为向量范数。

常见向量范数有：

• $L_1$ 范数 $\|x\|_1 = \sum_{i=1}^n|x_i|$
• $L_2$ 范数 $\|x\|_2 = \sqrt{\sum_{i=1}^n(x_i)^2}$
• $L_{\infty}$ 范数 $\|x\|_{\infty} = \max_{i}|x_i|$
• $L_p$ 范数 $\|x\|_p = (\sum_{i=1}^n|x_i|^p)^\frac{1}{p}$

$p = 1$ 时，$L_p$ 范数退化成 $L_1$ 范数；$p = 2$ 时，$L_p$ 范数退化成 $L_2$ 范数；$p \to \infty$ 时， 范数退化成 $L_{\infty}$ 范数。

任何两种向量范数都是等价的。

矩阵范数的定义。若对 $\forall A \in R^{n\times n}$ 都有一个实数 $\|A\|$ 与之对应，且满足：

1. 非负性：$当 A \ne 0 时，\|A\| \ge 0，当且仅当 A = 0时，\|A\| = 0$
2. 齐次性：$\forall \lambda \in R，\|\lambda A\| = |\lambda| \cdot \|A\|$
3. 三角不等式：$A,\ B \in R^{n\times n}，\|A+B\| \le \|A\| + \|B\|$
4. 相容性：$A,\ B \in R^{n\times n}，\|AB\| \le \|A\| \cdot \|B\|$

则称 $\|\ A\ \|$ 为 $R^{n\times n}$ 上的矩阵范数。

高数中的极值条件

$$\begin{align*} & f: R\to R \\ & \min f(x),\ s.t.\ x \in R \\ \end{align*}$$

• 一阶必要条件：$x^*\ 是极小值点 \Rightarrow f'(x) = 0$
• 二阶必要条件：$x^*\ 是极小值点 \Rightarrow f'(x) = 0,\ f''(x^*) \ge 0$，反过来不行，比如 $y=x^3$ 在 $x=0$ 处没有极小值
• 二阶充分条件：$f'(x) = 0,\ f''(x^*) > 0 \Rightarrow x^*\ 是极小值点$
• 充要条件：$f(x)可微凸，x^*\ 全局极小 \Leftrightarrow f'(x^*) = 0$，若 $f(x)$ 严格凸，则全局极小值唯一

拓展得到无约束优化问题的极值条件

最优化问题的模型

$$(p)\begin{cases} min. & f(x) \\ s.t. & g_i(x)\le0 & i=1,2,\cdots,m_i \\ & h_j(x)=0 & j=1,2,\cdots,m_j \\ & x\in X & X\subset R^n \end{cases}$$

其中，$x$是决策变量，$f(x)$ 是目标函数，$g_i(x)\le0$ 是不等式约束，$h_j(x)=0$ 是等式约束，$x\in X$ 是箱子集。后三者统称为“约束条件”。

满足约束条件的点是可行点。可行集（可行域）是全体可行点组成的集合，即$F=\{x\in R^n|g_i(x)\le0,i=1,2,\cdots,m_i, h_j(x)=0,j=1,2,\cdots,m_j, x\in X\}$。

全局极小点：对于$x^*\in F$，若对$\forall x \in F$，$f(x^*) \le f(x)$都成立，则称$x^*$为最优化问题(p)的全局极小点。

局部极小点：对于 $x^*\in F$ ，若存在 $x^*$ 的 $\varepsilon > 0$ 邻域 $N(x^*,\varepsilon)=\{x\mid\left | x^*-x \right | <\varepsilon\}$ ，使得对每个 $x \in F \cap N(x^*,\varepsilon)$ ，$f(x^*) \le f(x)$ 都成立，则称$x^*$为最优化问题(p)的局部极小点。

最优化问题的分类

1. 按约束分类

• 约束优化问题
• 箱子集约束优化问题
• 无约束优化问题

2. 按线性性质分类

• 线性规划问题：目标函数、约束函数都是线性函数
• 非线性规划问题：目标函数、约束函数存在非线性函数

3. 按决策变量的连续性分类

• 连续优化问题
• 离散优化问题，也叫组合优化
  • 整数规划问题
  • 0-1 规划问题，表示是否使用某项资源
• 混合整数规划问题：一部分变量连续，一部分变量离散

4. 按目标函数的个数分类

• 单目标规划问题：只有一个目标函数
• 多目标规划问题：多个目标函数

5. 按决策变量的随机性分类

• 确定性优化问题
• 随机优化问题
• 鲁棒性优化问题

凸集凸锥

约定两个符号的表示：

$$\begin{matrix} x^{(1)}, x^{(2)} & \in R^n \\ x_1, x_2 & \in R \end{matrix}$$

凸集的定义：设 $S$ 为 n 维欧式空间 $R^n$ 中一个集合。若对 $S$ 中任意两点，联接它们的线仍属于 $S$ 。换言之，对 $S$ 中任意两点 $x^{(1)}$，$x^{(2)}$ 及每个实数 $\lambda\in[0,1]$ ，都有 $\lambda x^{(1)} + (1-\lambda) x^{(2)} \in S$ ，则称 $S$ 为凸集。

规定，单点集 $\{x\}$ 为凸集，空集 $\varnothing$ 为凸集。

凸锥的定义：设集合 $C \subset R^n$，若对 $C$ 中每一点 $x$，当 $\lambda$ 取任何非负数时，都有 $\lambda x \in C$ ，则称 $C$ 为锥，又若 $C$ 为凸集，则称 $C$ 为凸锥。

规定，集合 $\{0\}$ 为凸锥，$R^n$ 为凸锥。

凸集的性质：

1)凸集的交集是凸集；（并集不是）
2)凸集的内点集是凸集；
3)凸集的闭包是凸集。
4)分离与支撑：凸集边界上任意点存在支撑超平面；两个互相不交的凸集之间存在分离超平面。
打个比方：内点集，橙子去掉皮后的部分；闭包，包括皮的橙子

凸集分离定理：

凸集分离定理，让我想起了感知机

闭凸集的一个性质

inf 是下确界，min 是最小值，inf 不一定能取到值，min 一定能取到值。类似的还有上确界 sup 和最大值 max。

铺垫凸集分离定理的提出，这部分看不懂，跳过

凸函数凸组合

最优化的凸函数定义与同济教程中的凸函数定义刚好相反。最优化中一般求最小值，从上往下看，图形应该是凸的。

凸函数的定义：设集合 $S \subset R^n$ 为凸集，函数 $f :S\to R$。若 $\forall x^{(1)},\ x^{(2)} \in S,\ \lambda \in (0,1)$ ，均有 $f(\lambda x^{(1)} + (1-\lambda))x^{(2)} \le \lambda f(x^{(1)}) + (1-\lambda)f(x^{(2)})$ ，则称 $f(x)$ 为凸集 $S$ 上的凸函数。

若进一步有上面不等式以严格不等式成立，则称 $f(x)$ 为凸集 $S$ 上的严格凸
函数。当 $-f(x)$ 为凸函数（严格凸函数）时，则称 $f(x)$ 为凹函数（严格凹函
数）。

直线也是凸函数，但不是严格凸函数。

凸函数的性质：设 $f_1,\ f_2$ 是凸函数，则 $\lambda_1 f_1 + \lambda_2 f_2$ 也是凸函数，该性质可以推广到有限个，比如 $\lambda_1 f_1 + \lambda_2 f_2 + \lambda_3 f_3$。

$$\begin{align*} & 证：\forall x^{(1)},\ x^{(2)},\ x^{(3)} \in S \\ & \lambda_1,\ \lambda_2,\ \lambda_3 \in R,\ \lambda_1,\ \lambda_2,\ \lambda_3 \ge 0,\ \lambda_1 + \lambda_2 + \lambda_3 = 1 \\ & f(\lambda_1x^{(1)} + \lambda_2x^{(2)} + \lambda_3x^{(3)}) \\ & = f(\lambda_1x^{(1)} + (1-\lambda_1)(\frac{\lambda_2x^{(2)}}{1-\lambda_1} + \frac{\lambda_3x^{(3)}}{1-\lambda_1})) \\ & \le \lambda_1f(x^{(1)}) + (1-\lambda_1)f(\frac{\lambda_2x^{(2)}}{1-\lambda_1} + \frac{\lambda_3x^{(3)}}{1-\lambda_1}) \\ & \le \lambda_1f(x^{(1)}) + \lambda_2f(x^{(2)}) + \lambda_3f(x^{(3)}) \\ \end{align*}$$

水平集的定义：设集合 $S\subset R$ ，函数 $f :S\to R$ ，$\alpha\in R$ ，称 $S_{\alpha} = \{ x\in S∣ f(x) \le \alpha \}$ 为 $f(x)$ 在 $S$ 上的 $\alpha$ 水平集。

水平集的性质：设集合 $S\subset R$ 是凸集，函数 $f :S\to R$ 是凸函数，则对 $\forall\alpha\in R$ ，$S_{\alpha}$ 是凸集。

凸组合的定义：设 $x^{(1)},\ x^{(2)},\ \dots\ ,\ x^{(m)} \in R^n,\ \lambda_j \ge 0,\ \sum_{j=1}^m \lambda_j = 1$，那么称 $\sum_{j=1}^m \lambda_jx^{(j)}$ 为 $x^{(1)},\ x^{(2)},\ \dots\ ,\ x^{(m)}$ 的凸组合。

• $\lambda_j \in R$ 时，构成线性组合，是线性子空间
• $\lambda_j \ge 0,\ \sum\lambda_j > 0$ 时，构成半正组合，是凸锥
• $\lambda_j \ge 0,\ \sum\lambda_j = 1$ 时，构成凸组合，是凸集

$S$ 是凸集 $\Leftrightarrow$ $S$ 中任意有限点的凸组合属于 $S$ 。
$C$ 是凸锥 $\Leftrightarrow$ $C$ 中任意有限点的半正组合属于 $C$ 。
$f(x)$ 为凸集 $S$ 上的凸函数 $\Leftrightarrow$ $S$ 上任意有限点的凸组合的函数值不大于各点函数值的凸组合。

方向导数：设 为非空凸集，函数 $f:S\to R$ ， 再设 $x^* \in S$ ， 为方向，使当 $\lambda > 0$ 充分小时有 $x^*+ \lambda d \in S$ ，如果 $\lim_{\lambda\to+0} \frac{[f(x^*+ \lambda d) － f(x^*)]}{\lambda} 存在(包括 \pm\infty)$ ，则称 $f(x)$ 为在点 $x^*$ 沿方向 的方向导数存在，记作 $f^′(x^*;d)$ 。若 $f(x)$ 在 $x^*$ 处可导，则 $f^′(x^*;d) = [\bigtriangledown f(x^*) ]^Td$ 。

凸函数的性质：设集合 $S$ 为凸集，函数 $f :S\to R$ 。$f(x)$ 为凸集 $S$ 上的凸函数。$x^*$为问题（fs ） 的 l.opt，则 $x^*$ 为 g.opt 。又如果 是严格凸函数，那么 $x^*$ 是（fs）的唯一 g.opt。

$$\begin{align*} & 证：反证法，假设存在 x 优于 x^* \Rightarrow f(x) < f(x^*),\ \forall \lambda \in (0,1),\\ & f(\lambda x + (1-\lambda)x^*) \\ & \le \lambda f(x) + (1-\lambda)f(x^*) \\ & < \lambda f(x^*) + (1-\lambda)f(x^*) = f(x^*) \\ & 令\ \lambda \rightarrow 0,\ f(x^*) < f(x^*),\ 假设错误，原命题成立 \\ & \\ & 证：反证法，假设存在另一个点 x \in S，使 f(x) = f(x^*),\ \forall \lambda \in (0,1),\\ & f(\lambda x + (1-\lambda)x^*) \\ & < \lambda f(x) + (1-\lambda)f(x^*) = f(x^*) \\ & 此时存在比 x^* 更小的点，假设错误，x^* 是（fs）的唯一全局最优解 \end{align*}$$

凸函数判别的一阶充要条件：设 $S$ 是开集（不包含边界点的集合），$f$ 在 $S$ 上可微，则 $f$ 是凸函数 $\Leftrightarrow \forall x,\ x^* \in S$，有 $f(x) \ge f(x^*) + \bigtriangledown f^T (x^*)(x-x^*)$ ；$f$ 是严格凸函数 $\Leftrightarrow \forall x,\ x^* \in S,\ x \ne x^*$ ，有 $f(x) > f(x^*) + \bigtriangledown f^T (x^*)(x-x^*)$

$$\begin{align*} & \Longrightarrow : \\ & \forall x,y \in S,\ \forall \lambda \in (0,1) \\ & \lambda f(x) + (1-\lambda)f(y) = {\color{Red}f(y) + \lambda(f(x)-f(y))} \\ & \ge f(\lambda x+(1-\lambda )y) = f(y+\lambda(x-y)) = {\color{Red}f(y) + \lambda\bigtriangledown^T f(y)(x-y) + o\|x-y\|} \\ & 可得\ f(x)-f(y) \ge \bigtriangledown^T f(y)(x-y) + \frac{o\|x-y\| \\}{\lambda} \\ & 令\ \lambda \to 0,\ f(x) \ge f(y) + \bigtriangledown^T f(y)(x-y),\ \forall y \in S \\ & \\ & \end{align*}$$

凸函数判别的二阶充要条件：设 $S$ 是开集，$f$ 在 $S$ 上二次可微，则 $f 凸 \Leftrightarrow \forall x \in S，\bigtriangledown^2 f(x)$ 半正定。若 $\forall x \in S，\bigtriangledown^2 f(x)$ 正定，则 $f$ 严格凸。

$$\begin{align*} & \Longleftarrow: \\ & \forall x,y \in S \\ & f(x) = f(y) + \bigtriangledown^Tf(y)(x-y) + \frac{1}{2}(x-y)^T\bigtriangledown^2(x_{\mu})(x-y),记\ x_{\mu} = y+\mu(x-y) \\ & 由半正定: \forall x \in R^n,\ x^TAx \ge 0 可得，\frac{1}{2}(x-y)^T\bigtriangledown^2(x_{\mu})(x-y) \ge 0 \\ & f(x) \ge f(y) + \bigtriangledown^Tf(y)(x-y) \\ & 由上一个证明可得，f 为凸函数 \\ & \\ & \Longrightarrow: \\ & \forall x,y \in S,\ \forall \lambda \in (0,1) \\ & f(\lambda x+(1-\lambda )y) = {\color{Red}f(y+\lambda(x-y))} \\ & = {\color{Red}f(y) + \lambda\bigtriangledown^T f(y)(x-y) + \lambda^2(x-y)^T\bigtriangledown^2(y)(x-y) + o(\lambda^2\|x-y\|^2)} \\ & 易得\ f凸 \Rightarrow f(x) \ge f(x^*) + \bigtriangledown f^T (x^*)(x-x^*)，\forall x \in S \\ & 可得\ \frac{\lambda^2(x-y)^T\bigtriangledown^2(y)(x-y) + o(\lambda^2\|x-y\|^2)}{\lambda^2} \ge 0 \\ & 令\ \lambda \to 0,\ (x-y)^T\bigtriangledown^2(y)(x-y) \ge 0 \Rightarrow \bigtriangledown^2 f(x) 半正定\\ \end{align*}$$

凸规划的定义：当 $(f\ S)$ 中，$S$ 为凸集，$f$ 是 $S$ 上的凸函数（求min）时，称$(f\ S)$ 为凸规划，即求凸函数在凸集上的极小点。对于 $(fgh)$ ，当 $f,\ g_i$ 为凸函数， $h_j$ 为线性函数时，$(fgh)$ 为凸规划。

凸规划的局部极小点就是全局极小点，且极小点的集合是凸集。

凸包的定义：设 $S \subset R^n$ 为非空集合（不一定是凸集），由 $S$ 中所有的有限点的凸组合所构成的集合，称为 $S$ 的凸包，记为 $cov(S)$ 。如果 $S$ 是凸集，则 $S = cov(S)$ 。

多面集的定义：有限个半空间的交 $S = \left\{x | Ax \le b \right\}$ 称为多面集，其中 $A$ 为 $m \times n$ 矩阵，$b$ 为 m 维向量。当 $b$ 为0时，$\left\{x | Ax \le 0 \right\}$ 表示凸锥。

多面集很像是约束条件方程组、非齐次线性方程组。

极点的定义：设 $S$ 为非空凸集，$x \in S$ ，若 $x$ 不能表示成 $S$ 中两个不同点的凸组合；换言之，若假设 $x = \lambda x^{(1)} + (1 - \lambda)x^{(2)} \ (\lambda \in (0,1)),\ x^{(1)},\ x^{(2)} \in S$ ，必推得 $x = x^{(1)} = x^{(2)}$ ，则称 $x$ 是凸集 $S$ 的极点。

已知 $x$ 为 $S$ 的极点，$\exists x^{(1)},\ x^{(2)} 为 S 的点，\lambda\in (0,1)，若x = \lambda x^{(1)} + (1-\lambda)x^{(2)}，则 x = x^{(1)} = x^{(2)}$

方向的定义：设 $S$ 为 $R^n$ 中的闭凸集，$d$ 为非零向量，如果对 $S$ 中的每一个 $x$，都有射线 $\{ x + \lambda d | \lambda \ge 0 \} \subset S$ ，则称向量 $d$ 为 $S$ 的方向。

已知 $d$ 为 $S$ 的极方向，$\exists d^{(1)},\ d^{(2)} 为 S 的方向，\lambda_1,\ \lambda_2 \ge 0，若d = \lambda_1 d^{(1)} + \lambda_2 d^{(2)}，则 d = d^{(1)} = d^{(2)}$

极方向的定义：设 $d^{(1)}$ 和 $d^{(2)}$ 是 $S$ 的两个方向，若对任何正数 $\lambda$ ，有 $d^{(1)} \ne \lambda d^{(2)}$ ，则称 $d^{(1)}$ 和 $d^{(2)}$ 是两个不同的方向。若 $S$ 的方向 $d$ 不能表示成该集合的两个不同方向的正的线性组合，则称 $d$ 为 $S$ 的极方向。

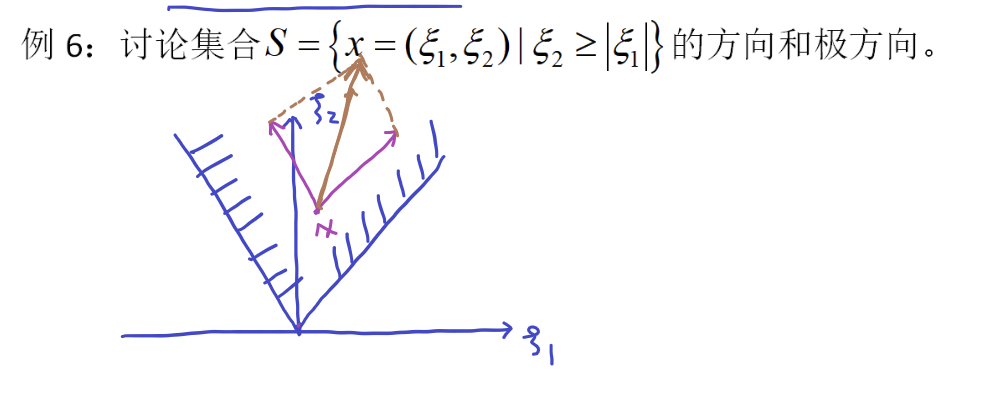
图中有两个标为红色的极方向

集合S表示的图形应当是有一侧没边的，如此就存在方向，即有界集不存在方向。平行于一侧边的方向是极方向。

用极点表示一些点（凸组合），在这些点上加一个方向，这个方向用极方向表示。

定理（极点特征）设 $A_{m\times n}$ 满秩，$x$ 是 $S$ 极点的充要条件是：存在分解 $A = (B,\ N)$ ，其中 $B$ 为 $m$ 阶非奇异矩阵（即可逆矩阵），使 $x^T = (x_B^T,\ x_N^T)$ ，这里 $x_B = B^{-1}b \ge 0,\ x_N = 0$ 。
注：$S$ 中必存在有限多个极点( $\le C_n^m$ ) 。

$$\begin{align*} & a\\ & \end{align*}$$

从6个可能的点中求极点，课件里只判断了3个点

定理 （极方向特征）设 $A = (a_1,\ a_2,\ \dots\ ,\ a_n)$ ，秩为 $m$
(1) $d$ 是 $S$ 方向的充要条件是 $Ad=0,\ 且d \ge 0$
(2) $d$ 是 $S$ 极方向的充要条件是：存在分解 $A = (B,\ N)$ ，其中 $B$ 为 $m$ 阶非奇异矩阵，对于 $N$ 中的列向量 $a_j$ ，使 $B^{-1}a_j \le 0,\ d^T = (d_B^T,\ d_N^T)$ ，这里 $d_B = -B^{-1}a_j \ge 0,\ d_N = (0,\ \cdots\ ,\ 1,\ \cdots\ ,\ 0)^T$ 。
注：S中必存在有限多个极方向 ( $\le (n－m)C_n^m$ ) 。

从30个方向中求极方向

极点：$x_B = B^{-1}b \ge 0,\ x_N = 0$
极方向：$d_B = -B^{-1}a_j \ge 0,\ d_N = e_j$

定理（表示定理）考虑多面体 $S = \{x\in R^n|Ax = b, x \ge 0\}$，设 $A$ 满秩，$x^{(1)} ,\ x^{(2)},\ \cdots\ ,\ x^{(k)}$ 为所有极点，$d^{(1)},\ d^{(2)},\ \cdots\ ,\ d^{(l)}$ 为所有极方向。那么，对于 $\forall x\in S,\ \exists\lambda_i \ge 0,\ i=1,\ 2,\ \cdots\ ,\ k$ ，且 $\lambda_1 + \lambda_2 +\cdots+ \lambda_k = 1,\ \mu_j \ge 0,\ j = 1,\ 2,\ \cdots\ ,\ l$ ，有 $x = \lambda_1x^{(1)} + \lambda_2x^{(2)} +\ \cdots\ + \lambda_kx_{(k)} + \mu_1d^{(1)} + \mu_2d^{(2)} +\ \cdots\ + \mu_ld^{(l)}$ 。

线性规划

不可能找到进基变量使目标函数再下降了，迭代终止，找到最优解。

对于 $z_j - c_j \le 0$ ，$x_j$ 仍然保持为0
对于 $z_j - c_j > 0$ ，取 $z_k - c_k = \underset{z_j-c_j>0}{max}\{z_j-c_j\} = \underset{j\in R}{max}\{z_j-c_j\}$

$Ax=b$ 解的变化：
$x_B = B^{-1}b - B^{-1}Nx_N \xrightarrow{x_k由0变正以后} x_B = B^{-1}b - B^{-1}P_kx_k \xrightarrow[令\bar{b}=B^{-1}]{令y_k=B^{-1}P_K} x_B = \bar{b} - y_k x_k$
其中，$B^{-1}$ 形状为 $m\times m$ ，$N$ 形状为 $m \times (n-m)$ ，$B^{-1}N$ 形状为 $m \times (n-m)$ ，$x_N$ 形状为 $(n-m) \times 1$，是零向量。$x_k$ 变正以后，$B^{-1}N$ 的第$k$ 列保留下来，作为 $P_k$ 。

$$\begin{align*} & x_B = \begin{pmatrix} x_{B_1} \\ x_{B_1} \\ \vdots \\ & x_{B_m}\end{pmatrix} = \begin{pmatrix} \bar{b}_1 \\ \bar{b}_2 \\ \vdots \\ \bar{b}_m \end{pmatrix} - \begin{pmatrix} y_{1k} \\ y_{2k} \\ \vdots \\ y_{mk} \end{pmatrix} x_k \\ & x_N = (0 \quad \cdots \quad 0 \quad x_k \quad 0 \quad \cdots \quad 0)^T \\ & f = f_0 - (z_k - c_k)x_k \\ & x_B \ge 0, z_k - c_k > 0, x_k > 0 \end{align*}$$

1. $x_k$ 越大，函数值下降越多。
2. 若 $y_{ik} \le 0, \forall x_k$
3. 若 $y_{ik} > 0$，$x_k$ 不能无限增大，否则 $x_B = \bar{b} - y_k x_k < 0$ ，不可行

综上，$x_k$ 应选取满足 1、3 的最大值

r 为出基下标，k 为进基下标

可证明：新可行解 $x = ()$ 是基本可行解

对应基变量的判别数总是小于等于

尾声

缺少一部分证明，大概一页草稿纸多一点的样子。

缺少线性规划部分的证明和应用，这部分听完课再补上。